Most languages include bitwise operations like logical AND, OR, XOR, inversion, and shift left/right operators. And most of these are just barely evolved beyond the level of assembly language operators that perform the same. TODO: mention compilers.
Meanwhile, other aspects of programming have ascended the abstraction ladder, allowing higher-level concepts to be expressed in a more “natural” way (while underlying compilers continue to crank out impressively optimized machine-level code). Some examples of this are the broader functional programming movement, list comprehensions in Python, and (my favorite) for comprehensions in Scala.
This post sketches out some ideas originating with this tweet, and may change with new updates and ideas. Please add your comments below.
If you described some common bitwise structures, such as you might run into in embedded programming, you’d say something like
In the top 5 bits, you put the identifier, and in the remaining 11 bits, you put the payload. (Implied: the overall size is 5+11=16 bits wide)
Or on a whiteboard:
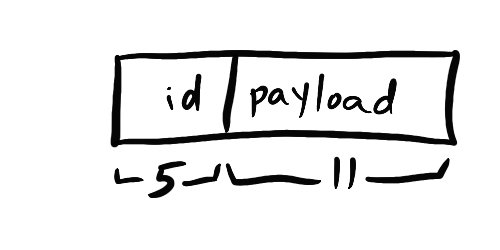
A huge chunk of bitwise operations can be divided into two categories. There are definitely other things that can be done, but the most common ones can be built from these two building blocks.
- Packing: taking program variables, and packaging them within specific bit boundaries
- Unpacking: starting with a structured sequence of bits, unpack them into usable program variables
It’s tempting to think about language features that already exist in some languages to convert numeric values into an array or stream of booleans. From there, existing array or stream operations can work their magic. This is actually an underused technique but it comes with a lot of overhead. What I’m looking for is a syntax a compiler can convert into high-quality machine language like what you might hand-write.
First, unpacking. If someone hands you a unsigned sixteen-bit array (called UINT16) called “input”, populated as described above, and you need to unpack it into program variables for id and payload, you’d have to write code like this, in a generic Java-like syntax.
int payload = input & 0x7ff
// For id, we need to mask off the other bits, and shift them down to values 0-31
// it is tempting to do this:
// int id = (input & 0xf8) >> 11
// but it is more common in practice to flip the order of operations, for reasons explained below
int id = (input >> 11) & 0x1f;To unpack the payload value, we need to “mask” out the unwanted bits. This is done with the magic number 0x7ff, or in binary, 0b0000011111111111. That’s eleven “1”s in the lower position, zeroes in the rest. A logical AND of anything with zero is zero, so anything in those upper bits gets “masked”, leaving just the lower bits in place. Assigning this masked value to the variable payload gets us exactly what we want.
To extract the id in the top five bits, we need to mask those bits away, but masking alone isn’t enough. Suppose all five bits of the id were 1s, representing a value of 31. Even with all the lower bits masked away, the value in binary is still 0b1111100000000000, or in decimal, 63,488. Oops. You can imagine picking up those five bits and “right shifting them (with zeros filling on on the left) until the number looks like 0b0000000000011111, or in decimal, 31, the correct and desired id value. And don’t forget the parentheses for clarity in otherwise confusing and magic-number-ridden code.
Packing has its own quirks. Let’s add a new variable called output and populate it.
UINT16 output = ((id & 0x1f) << 11) | (payload)Again, masking and shifting the id value, sharing the same magic number of 0x1f as before, because this time we need to make sure the value fits in the 5-bit range, then left shift it into place. There’s a logical OR in there for the 11-bit payload value too. Commonly you’ll see an ordinary + operator instead, which does the same thing except when it doesn’t. (And did you catch the bug? This code never checks the payload for overflow. Any value that doesn’t fit in the 11 bits will spill over and bork the id.)
If you don’t look at these all the time, you might need to interrupt your thought process to think about what’s going on, to pause and mentally translate between ‘human’ (as above) and ‘machine’. Maybe you like interrupting your main line of thought to solve a tiny Sudoku before every once in a while, but I hate it. We use higher-level languages to free ourselves to think at a higher level.
So why not have a language construct that makes it obvious how to destructure a value–typically a fixed-length integer–into bits, and reassemble them as needed? If you look at datasheets and bit-level protocol specifications, you will usually see little diagrams showing bit locations and the like. Using these as inspiration, can we set up a way for a programming language to describe the outcome of a bit operation without getting bogged down in details? Leave the details for the compiler or interpreter. Let’s jump into an example.
// unpacking
unpack input[id:5, payload:11] {
local_id = id;
local_payload = payload;
}
// in languages that directly support destructuring, it could work like
// local_id, local_payload = unpack input [id:5, payload:11]
//packing
int16 output = pack [local_id:5, local_payload:11];The ‘unpack’ statement works much like ‘for’ in C or Java. It takes a descriptive block–that I suppose could be called a bitmap–that kind of looks like what you’d see on a datasheet or RFC, and then a code block to do something with the divided-up pieces. Within the bitmap, different bit ranges are assigned temporary identifiers as well as bit-widths, and the associated code block can do something with it. If you were whiteboarding, you’d draw basically this (which we did, in the earlier part of this post).
Packing uses a similar construct, but with a pack statement that returns a value.
It’s pretty common to unpack and then repack in the same logical operation. Myearlier post had code that did this, applying a scaling factor to each rgb byte in a 32 bit int. Depending on the underlying components, sometimes you need to swap the r and g bytes too. Maybe it’s overthinking, but it would be nice if there was a way to avoid instantiating all the temporary intermediate values in that case. Maybe something like:
UINT32 input ... // packed 32-bit value
float c = 0.5; // multiplier between 0 and 1
UINT32 output =
unpack input[_, g:8, r:8, b:8] {
pack [_, r*x:8, g*x:8, b*x:8];
};The variables r,g,b have no scope or meaning outside the curlies. They exist solely to populate the following expression, where they are reassembled. Based on the bit width specifiers, there’s no ambiguity about types; no need for casting. The _ marker means “whatever’s left over” or maybe “don’t care” since there we only ever touch or look at 24 of the 32 bits. A return statement lets the overall code block return a value.
A couple more examples. Everything here is basically endian-independent. Just like with the raw shift operators << and >>, the shifting happens against the value of the variable, not the underlying representation. About the only time endianness comes up is when taking a larger unit, like a UINT32, and treating just part of it as a UINT8. Anyway, endian flipping is pretty straightforward:
UINT32 byteflipped = unpack input32[a:8, b:8, c:8, d:8] {
pack [d:8, c:8, b:8, a:8];
};Similar could be used to flip bit order.
UINT8 bitflipped = unpack input8[a:1, b:1, c:1, d:1, e:1, f:1, g:1, h:1] {
pack [h:1, g:1, f:1, e:1, d:1, c:1, b:1, a:1];
};At this point, one wonders whether some kind of array syntax would be better, but it’s probably better to keep it simple to star out.
There’s lots of ways to complect this further, but this seems like a pretty useful starting point. An important part of the idea here is that after compilation, you would end up with the exact same optimized code as the handwritten examples shown earlier.
What do you think? Any language designers or fans want to weigh in?